learn
Le perceptron
Définition
Le perceptron, ou neurone formel, est un neurone artificiel. Il sert à faire de l’apprentissage supervisé. Inventé en 1957 par Frank Rosenblatt, il peut résoudre des problèmes linéairement séparable, comme l’opération AND.
Comment ça marche
Un perceptron prend des entrées $( x_1, x_2, \dots, x_n $), leur associe des poids $( w_1, w_2, \dots, w_n $), et calcule une sortie. Voici les étapes :
- Somme pondérée : On calcule ( $z = \sum_{i=1}^{n} w_i x_i + b$ ), où $( b $) est le biais.
- Fonction d’activation : On applique une fonction, souvent la fonction en échelon : $f(z) = \begin{cases} 1 & \text{si } z \geq 0 \ 0 & \text{sinon} \end{cases}$ La sortie est ( $y = f(z)$ ).
Illustration
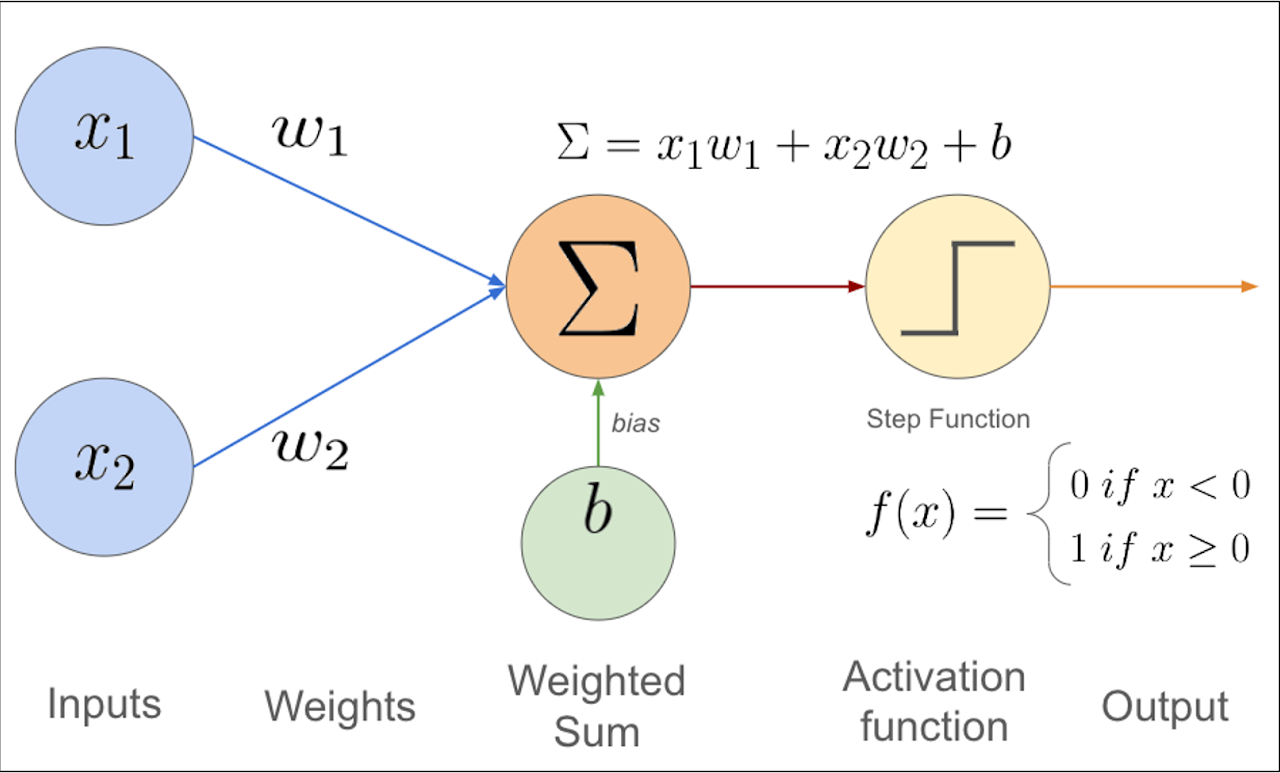
Apprentissage
Pour apprendre, le perceptron ajuste les poids et le biais :
- On commence avec des poids aléatoires.
- Pour chaque exemple $(x, y_{\text{vrai}}) $, on prédit $y_{\text{prédit}}$.
-
Si la prédiction est fausse, on met à jour : $w_i \gets w_i + \eta (y_{\text{vrai}} - y_{\text{prédit}}) x_i$
$b \gets b + \eta (y_{\text{vrai}} - y_{\text{prédit}})$
où $(\eta$) est le taux d’apprentissage (ex. : 0.1).
Exemple : AND
Pour l’opération AND avec deux entrées $( x_1, x_2 \in {0, 1} $):
| $( x_1 $) | $( x_2 $) | Sortie (AND) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Le perceptron trouve des poids (ex. : $( w_1 = 0.5, w_2 = 0.5, b = -0.7 $)) pour résoudre ce problème.
Limites
Le perceptron ne peut résoudre que des problèmes linéaires. Par exemple, il échoue sur XOR :
| $( x_1 $) | $( x_2 $) | Sortie (XOR) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
C’est parce que XOR n’est pas linéairement séparable.
Lien avec Deep Learning
Le perceptron est la base des réseaux de neurones. En combinant plusieurs perceptrons, on peut résoudre des problèmes complexes, comme en Deep Learning ou en robotique.
Exemple en C
/*
* Copyright (c)
* 2025 NotPunchnox
*/
// Importation de la lib math
#include <stdio.h>
#include <math.h>
// Fonciton de calcul du taux d'erreur ( Log vraisemblance négative )
// formule: -(sortie_attendue * log(prediction) + (1 - sortie_attendue) * log(1 - prediction))
double Loss(double prediction, double sortie_attendue) {
double result = -(sortie_attendue * log(prediction)) + ((1 - sortie_attendue) * log(1 - prediction));
return result;
}
// Fonction d'activation ( sigmoïde )
double activation(double y) {
return 1 / (1 + exp(-y));
}
// Fonction principale
int main() {
// Déclaration des variables
// exemples de données sur l'opérateur logique AND
double x[4][2] = {
{0, 0},
{0, 1},
{1, 0},
{1, 1}
};
double yy[4] = {
0, // 0 AND 0 = 0
0, // 0 AND 1 = 0
0, // 1 AND 0 = 0
1 // 1 AND 1 = 1
};
double w[2] = {0.5, -1};
double b = 1;
double learning_rate = 0.1;
// Boucle d'entrainement
for (int epoch = 0; epoch < 5000; epoch++) {
// boucle sur les données
for (int i = 0; i < sizeof(x) / sizeof(x[0]); i++) {
// Calcul de la sortie du perceptron
double y = (x[i][0] * w[0]) + (x[i][1] * w[1]) + b;
double p = activation(y);
double error = Loss(p, yy[i]);
// Mise à jour des poids et du biais
for (int j = 0; j < sizeof(w) / sizeof(w)[0]; j++) {
w[j] = w[j] - learning_rate * (p - yy[i]) * x[i][j];
}
// Mise à jour du biais
b = b - learning_rate * (p - yy[i]);
}
// Affichage des poids et du biais
printf("Epoch %d: w1 = %f, w2 = %f, b = %f\n", epoch, w[0], w[1], b);
}
// Affichage des poids finaux
printf("Final weights: w1 = %f, w2 = %f, b = %f\n", w[0], w[1], b);
// Test du perceptron sur les données d'entrainement
for (int i = 0; i < sizeof(x) / sizeof(x[0]); i++) {
double y = (x[i][0] * w[0]) + (x[i][1] * w[1]) + b;
double p = activation(y);
printf("Input: (%f, %f) => Prediction: %f, Expected: %f\n", x[i][0], x[i][1], p, yy[i]);
}
return 0;
}